Rajasthan Board RBSE Class 12 Maths Chapter 8 Application of Derivatives Ex 8.2
RBSE Solutions For Class 12 Maths Chapter 8.2 Question 1.
Prove that f(x) = x2 is increasing in interval (0, ∞) and decreasing in interval (-∞,0).
Solution:
Let x1, x2 ∈ [0,∞] is such that
x1 < x2
∴ x1 < x2 ⇒ x12< x1x2 …..(i)
and x1 < x2 ⇒ x1x2 < x22……(i)
From (i) and (ii),
x1 < x2 ⇒ x12 < X22
⇒ f(x1) < f(x2)
∴ X1 < X2 ⇒ f(x1) < f(x2)
where x1, x2 ∈ [0, ∞]
Hence, f(x) is continuously increasing in [0, ∞)
Again, let x1, x2 ∈ (-∞, 0) is such that
x1 < x2
Then
x1 < x2 ⇒ x12> x1x2
[∵ – 3 < – 2, (- 3) (- 3) = 9
(- 3) × (- 2) = 6
∴ 9 > 6
x12 > x1 x2]
Again
x1 < x2 ⇒ x1x2 > x22
Again – 3 < – 2
(- 3) × (- 2) = 6
(- 2) × (- 2) = 4
6 > 4
∴ x1x2 > x22]
From (i) and (ii),
x1 < x2 ⇒ X12 > x22
⇒ f(x1) > f(x2)
∴ x1 < x2 ⇒ f(x1) > f(x2)
Hence, f(x) is continuously decreasing in (-∞, 0).
Exercise 8.2 Class 12 Maths RBSE Question 2.
Prove that f(x) = ax, 0 < a < 1, is decreasing in R.
Solution:
Let x1,x2 ∈R is such that
x1 < x2
Then, x1 < x2
⇒ ax1 > ax2
[∵ 0 < a < 1 and x < x2 ⇒ ax1 > ax2]
⇒ f(x1) > f(x2)
∴ x1 < x2
⇒ f(x1) > f(x2) ∀ x1, x2 ∈ R
Hence, function f(x) = ax, 0 < a < 1, R is decreasing in R.
RBSE Solutions For Class 12 Maths Chapter 8 Question 3.
f(x) = log sin x, x ∈ (0,\(\frac { \pi }{ 2 } \))
Solution:
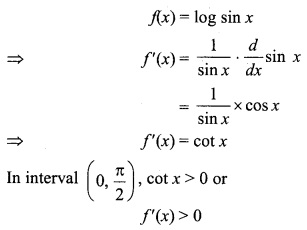
Hence, in interval (0,\(\frac { \pi }{ 2 } \)) function is continuously increasing
RBSE Solutions For Class 12 Maths Chapter 8 Exercise 8.2 Question 4.
f(x) = x100 + sin x + 1- x ∈ (0,\(\frac { \pi }{ 2 } \))
Solution:
f(x) = x100 + sin x + 1
Diff. w.r.t. x,
f'(x) = 100x99 + cos x
In interval (0,\(\frac { \pi }{ 2 } \))
f'(x) = 100x99 + cos x > 0
[∵ cos x > 0 and 100x99 > 0]
⇒ f'(x) > 0
Hence, function in interval (0,\(\frac { \pi }{ 2 } \)) is increasing.
RBSE Solutions For Class 12 Maths Chapter 8 Miscellaneous Question 5.
f(x) = (x – 1)ex + 1, x > 0.
Solution:
f(x) = (x – 1)ex+1
Diff. w.r.t. x,
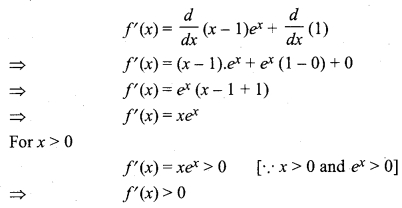
Hence, at x = 0, function is increasing.
12th Class RBSE Solution Question 6.
f(x) = x3 – 6x2 + 12x – 1,x ∈ R.
Solution:
f(x) = x3 – 6x62 + 12x – 1
DifF. w.r.t x,
f'(x) = 3x2 – 12x + 12
⇒ f'(x) = 3(x2 – 4x + 4)
⇒ f'(x) = 3(x – 2)2
⇒ f'(x) = 3(x – 2)2 ≥ 0
⇒ f'(x) ≥ 0 [∵(x – 2)2 > 0]
Hence, function f(x) is increasing in R.
RBSE Class 12 Maths Chapter 8 Question 7.
f(x) = tan-1 x – x, x ∈ R.
Solution:
f(x) = tan-1 x – x
Diff. w.r.t. x,
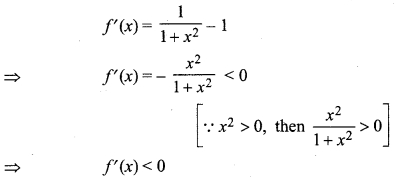
Hence, function fix) decreasing in R.
12th Maths RBSE Solution Question 8.
f(x) = sin4 x + cos4 x, x ∈(0,\(\frac { \pi }{ 4 } \))
Solution:
f(x) = sin4 x + cos4 x
Diff. w.r.t x,
f'(x) = 4 sin3 x cos x + 4 cos3 x(-sin x)
⇒ f'(x) = 4 sin x cos x (sin2 x – cos2 x)
⇒ f'(x) = -2.2 sin x cos x (cos2 x – sin2 x)
⇒ f'(x) = – 2sin 2x cos 2x
⇒ f'(x) = – sin 4x
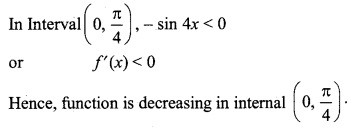
Class 12 Maths 8.2 Solutions Question 9.
f(x) = \(\frac { 3 }{ x } \) + 5, x ∈ R, x ≠ 0.
Solution:
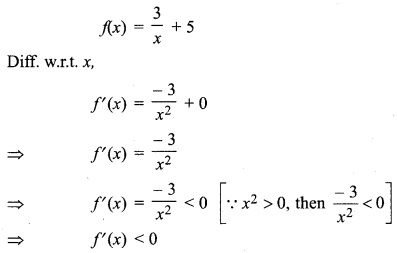
Hence, function f(x) is decreasing in x ∈ R when x ≠ 0.
Exercise 8.2 Class 12 Maths Question 10.
f(x) = x2 – 2x + 3, x < 1.
Solution:
f(x) = x2 – 2x + 3
Diff. w.r.t. x,
f'(x) = 2x – 2
⇒ f'(x) = 2(x – 1)
⇒ f'(x) = 2(x – 1) < 0 [When x < 1]
⇒ f'(x) < 0
Hence function f(x) is decreasing in interval x < 1.
Class 10 Maths Ex 8.2 Question 11.
f(x) = 2x3 – 3x2 – 36x + 7
Solution:
Given
f(x) = 2x3 – 3x2 – 36x + 7
⇒ f'(x) = 6x2 – 6x – 36
f'(x) = o
⇒ 6x2 – 6x – 36 = 0
⇒ 6(x2 – x – 6) = 0
⇒ 6(x – 3) (x + 2) = 0
⇒ x – 3 = 0 or x + 2 = 0
⇒ x = 3 or x = -2
Hence, point x = – 2, x = 3 divides the real number line into three intervals (-∞,-2), (-2, 3) and (3,∞).
(a) For (-∞, -2) interval.
f'(x) = 6x2 – 6x – 36 > 0
∵ At x = – 3
f'(x) = 6(- 3)2 – 6(- 3) – 36
= 6 × 9 + 6 × 3 – 36
= 54 + 18 – 36 = 36 >0
So,f'(x) > 0 can be shown like this by taking other points. Hence, function is continuously increasing in interval (-∞, – 2).
(b) For (-2, 3)
f'(x) = 6x2 – 6x – 36 < 0
∴ At x = 1
f'(x) = 6(1)2 – 6 × 1 – 36
= 6 – 6 – 36 = -36 < 0
At x = 0, f'(x) = 6(0)2 – 6 × 0 – 36
= – 36 < 0
So,f'(x) < 0 can be shown like this by taking other points.
Hence, function is continuously decreasing for x ∈ (- 2, 3).
(c) For (3, ∞)
f'(x) = 6x2 – 6x – 36 > 0
∵ At x = 4,
f'(x) = 6 × (4)2 – 6 × 4 – 36
= 96 – 24 – 36
= 96 – 60 = 36 > 0
At x = 5, f'(x)= 6(5)2 – 6 × 5 – 36
= 6 × 25 – 30 – 36
= 150 – 30 – 36
= 84 > 0
So,f'(x) > 0 can be shown like this for other points.
Hence, function f(x) is continuous increasing in interval
(-∞, -2) ∪ (3,∞). {∵ f'(x) > 0}
Function is continuously decreasing in interval (- 2, 3).
8.2 Class 10 Question 12.
f(x) = x4 – 2x2.
Solution:
Given
f(x) = x4 – 2x2
f'(x) = 4x63 – 4x (∵f(x) = 0)
⇒ 4x3 – 4x = 0
⇒ 4x(x2 – 1) = 0
⇒ 4x = 0 or x2 – 1 = 0
⇒ x = 0 or x = ± 1
Here, point x = 0, 1, – 1 divides real number line into four interval (-∞, -1), (-1, 0), (0, 1) and (1,∞).
(a) For interval (-∞, -1)
f'(x) = 4 x3 – 4x
At x = – 2, f'(x) = 4 x (- 2)3 – 4(- 2)
= -32 + 8 = -24 < 0
Like this it can be shown for other points (f'(x) <0).
(b) For interval (-1,0)
f'(x) = 4x3 – 4x
For x = -0.5
f'(x) = 4 × (- 0.5)3 – 4 × (- 0.5)
= -0.5 + 2.0 = 1.5 >0
Like this it can be shown for other points {f'(x) > 0}
(c) For interval (0, 1)
f'(x) = 4x3 – 4x
For x = 0.5
f'(x) = 4 × (0.5)3 – 4 × (0.5)
= 4 × 0.125 – 2.0
= 0.5 – 2.0 = – 1.5 < 0
Like this it can be shown for other points {f'(x)< 0}
(d) For interval (1, ∞)
f'(x) = 4x3 – 4x
For x = 2 f'(x) = 4 × (2)3 – 4 × 2
= 32 – 8 = 24 > 0
Like this it can be shown for other points {f'(x) > 0}
Hence, function is decreasing in interval (-∞, – 1) ∪ (0, 1) and function is increasing in interval (-1, 0) ∪ (1, ∞).
Question 13.
f(x) = 2x3 – 9x2 + 12x + 5.
Solution:
Given
f(x) = 2x3 – 9x2 + 12x + 15
f'(x) = 6x2 – 18x + 12
= 6(x2 – 3x + 2)
x = 1 and x = 2 divides the real number line into three intervals (-∞, -1), (1, 2) and (2,∞).
when x ∈ (-∞, 1) then f'(x) = + ve
when x ∈ (1,2) then f'(x) = – ve
when x ∈ (2,∞) then f'(x) = + ve
So, function is increasing in interval (-∞, 1) ∪ (2,∞) and decreasing in interval (4, 2).
Question 14.
f(x) = – 2x3 + 3×2 + 12x + 5.
Solution:
Given, f(x) = -2×3 + 3×2 + 12x + 5
f'(x) = – 6x2 + 6x + 12
= – 6(x2 – x – 2)
= – 6(x – 2)(x + 1)
x = – 1 and x = 2 divides the real number line into three intervals (-∞, -1), (- 1, 2) and (2,∞).
when x ∈ (-∞,-1), then f'(x) = -ve
when x ∈ (-1,2), then f'(x) = +ve
when x ∈ (2,∞), then f'(x) = -ve
So, function is increasing in interval (-1, 2) and decreasing in interval (-∞, -1) ∪ (2,∞).
Question 15.
Find the minimum value of a, such that function f(x) = x2 + ax + 5, is increasing in interval [1, 2]
Solution:
f(x) = x2 + ax + 5
⇒ f'(x) = 2x + a
x ∈ [1, 2]
⇒ 1 ≤ x ≤ 2
⇒ 2 ≤ 2x ≤ 4
⇒ 2 + a ≤ 2x + a ≤ 4 + a
⇒ 2 + a ≥ 0
⇒ a ≥ -2
Hence, minimum value of a is – 2.
Question 16.
Prove that, function f(x) = tan-1 (sin x + cos x), is increasing function in interval (0,\(\frac { \pi }{ 4 } \))
Solution:
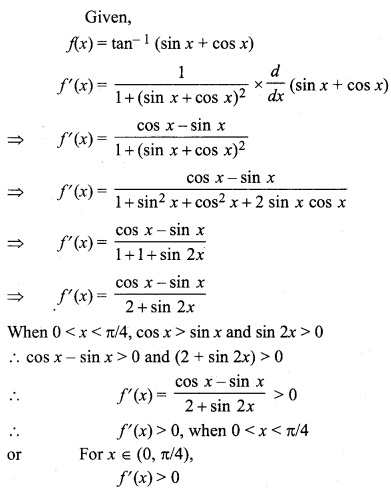
Hence, function is continuously increasing in interval (0, π/4).